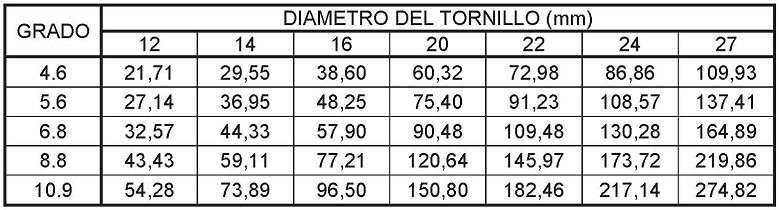
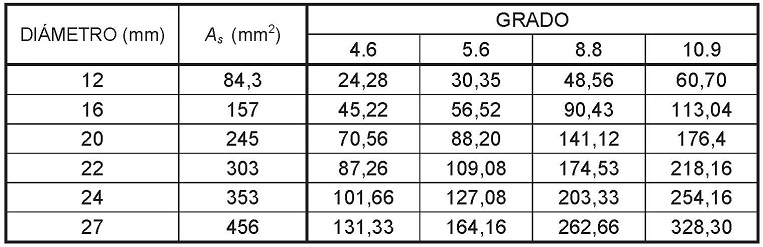

Los tornillos de clase 8.8 y 10.9 o superior son denominados también "tornillos de alta resistencia", siendo los "tornillos ordinarios" las demás de clase inferior.
γMb : Resistencia de tornillos 1,25
Si el plano de corte pasa por la parte roscada del tornillo:
- Grados 4.6, 5.6 y 8.8:
| Fv,Rd = | 0,6 * fub * As |
——————
| |
| γMb |
- Grados 4.8, 5.8, 6.8 y 10.9:
| Fv,Rd = | 0,5 * fub * As |
——————
| |
| γMb |
Si el plano de corte pasa por la parte no roscada del
tornillo:
| Fv,Rd = | 0,6 * fub * A |
——————
| |
| γMb |
| Fb,Rd = | 2,5 * α * fu * d * t |
—————————
| |
| γMb |
siendo α el menor valor de:
| e1 | , ó bien |
——
| |
| 3 * d0 |
| p1 | - | 1 | , ó bien |
——
|
—
| ||
| 3 * d0 | 4 |
| fub | , ó bien 1,0 |
——
| |
| fu |
donde:
d: diámetro del tornillo;
t: espesor de la chapa;
e1: distancia al extremo frontal;
d0: diámetro del agujero;
p1: separación entre tornillos;
As: área resistente a tracción;
A: área de la sección transversal
La resistencia a tracción de la unión tornillo-placa
Bt,Rd se tomará como la menor de la resistencia a tracción de
cálculo Ft,Rd y la resistencia a punzonamiento entre la
cabeza del tornillo y la tuerca Bp,Rd
| Ft,Rd = | 0,9 · fub · A |
——————
| |
| γMb |
| Bp,Rd = | 0,6 · π · dm · tp · fu |
——————————
| |
| γMb |
donde:
Bt,Rd: resistencia a tracción de la unión
tornillo-placa;
Bp,Rd: resistencia al punzonamiento de la
chapa;
fu: resistencia última de la chapa;
dm: menor media de la dimensión entre caras y
entre vértices de la cabeza del tornillo o tuerca;
tp: espesor de la placa bajo la cabeza del
tornillo o bajo la tuerca.
Los tornillos solicitados a cortante y axil al mismo tiempo
deben cumplir lo siguiente:
| Fv,Sd | + | Ft,Sd | ≤ | 1,0 |
———
|
————
| |||
| Fv,Rd | 1,4 · Ft,Rd |
La resistencia a deslizamiento de cálculo
Fs,Rd de un tornillo pretensado de alta resistencia se
tomará como:
| Fs,Rd = | ks · n · μ | · | Fp,Cd |
—————
|
|||
| γMb |
siendo Fp,Cd el esfuerzo de pretensazo que
viene dado por:
Fp,Cd =0,7 · fub ·
As
donde,
ks toma los siguientes valores:
1,0 ... para el caso de agujeros con holguras
nominales estándar
0,85 ... para el caso de agujeros a sobremedidas o
alargados cortos
0,7 ... para el caso de agujeros en ranuras
largos
n ... es el número de superficies en contacto entre las
chapas de la unión.
μ ... es el coeficiente de rozamiento, que toma los
siguientes valores:
μ = 0,5 para superficies de clase A
μ = 0,4 para superficies de clase B
μ = 0,3 para superficies de clase C
μ = 0,2 para superficies de clase D
siendo,
Superficies de clase A: son superficies limpiadas con chorro de
granalla o arena, con eliminación de partes oxidadas y sin picaduras o
metalizadas con aluminio proyectado.
Superficies de clase B: son superficies limpiadas con chorro de
granalla o arena, y pintadas con un silicato alcalino de cinc que produzca una
capa de espesor 50-80µm.
Superficies de clase C: son superficies limpiadas con cepillos
metálicos o por limpieza con llama, con eliminación de partes oxidadas.
Superficies de clase D: son superficies no tratadas.
Por último, γMb toma los siguientes
valores,
γMb = 1,25 Estado límite último
γMb = 1,10 Estado límite de servicio
γMb = 1,40 ELU en agujeros con ranura paralela
al esfuerzo
Si una unión resistente al deslizamiento se ve sometida a un
esfuerzo axil Ft simultáneo con un esfuerzo cortante
Fv que tienda a producir deslizamiento, la resistencia a
deslizamiento por cada tornillo se tomará como sigue:
- Categoría B (Resistente a deslizamiento en ELS):
| Fs,Rd,ser = | ks · n · μ | · | ( Fp,Cd - 0,8 · Ft,Sd,ser ) |
—————
| |||
| γMs,ser |
- Categoría C (Resistente a deslizamiento en ELU):
| Fs,Rd = | ks · n · μ | · | ( Fp,Cd - 0,8 · Ft,Sd ) |
—————
| |||
| γMs,ult |
a) Uniones atornilladas no pretensadas:
Para los tornillos de uniones no pretensadas el par de apriete
necesario será aquel que logre la condición de contacto ajustado de las
superficies alrededor de la zona de contacto de cada tornillo.
La condición de contacto ajustado se considera que es el
proporcionado por un operario utilizando una llave o herramienta normal sin
prolongador, o equivalente al punto en que una llave neumática empieza a
impactar.
Para conseguir una buena condición de contacto es aconsejable
proceder a un apretado progresivo de tornillos desde los más interiores hacia
fuera.
b) Uniones atornilladas pretensadas:
Para las uniones pretensadas se usarán los tipos de tornillos
8.8 y 10.9 o superiores, de acuerdo a la clasificación indicada en
el apartado 2 "Clases de tornillos" de este tutorial.
El pretensado se realizará una vez obtenida la condición de
contacto ajustado y se realizará de forma ordenada y progresiva entre todos los
tornillos que constituyen la unión.
El esfuerzo de pretensado (N0) que debe
obtenerse en la espiga del tornillo se corresponde al 70% de la resistencia a
tracción (fub) multiplicada por su área resistente (As)
de la sección del tornillo:
N0 = 0,7 · fub · As
Los valores de la resistencia a tracción (fub)
de los tornillos se pueden consultar en el apartado 2 "Clases de tornillos" de
este tutorial.
Los valores del área resistente a tracción
(As) de cada tornillo se pueden consultar en el apartado 5
"Dimensiones geométricas de los tornillos" del Tutorial Nº 31.
La siguiente tabla indica los valores del esfuerzo de pretensado
(N0) mínimo necesario para cada tornillo, según su diámetro y
clase.
|
Tabla A.
Esfuerzo de pretensado mínimo, N0
(kN)
| ||||||||
|
|
Diámetro del
tornillo (mm)
| |||||||
|
|
12
|
16
|
20
|
22
|
24
|
27
|
30
|
36
|
|
Tipo
de tornillo 8.8
|
47
|
88
|
137
|
170
|
198
|
257
|
314
|
458
|
|
Tipo
de tornillo 10.9
|
59
|
110
|
172
|
212
|
247
|
321
|
393
|
572
|
Este esfuerzo de pretensado debe conseguirse con una llave
dinamométrica que indique el par torsor aplicado durante el apriete del
tornillo.
Efectivamente, cuando se emplea una llave dinamométrica para
aplicar un par que apriete al tornillo, este par induce un esfuerzo de
pretensado (N0) en la espiga del tornillo, esfuerzo que va a
depender del diámetro del tornillo y de un coeficiente que marque el rozamiento
entre los componentes de la parte que gira.
Para el caso concreto de un estado de suministro de tuerca y
tornillo ligeramente engrasados, el par de apriete o torque que habrá que
aplicar con la llave dinamométrica, será el que resulte de aplicar la siguiente
expresión:
Mt = 0,18 · d · N0
donde,
Mt, el torque o par de apriete necesario
aplicar al tornillo (expresado en N·m)
d, es el diámetro del tornillo (expresado en
metros)
N0, es el esfuerzo de pretensado, indicado
en la Tabla A anterior según el diámetro y tipo de tornillo.
La ejecución de agujeros para tornillos deberá efectuarse
preferentemente mediante taladro. No obstante, se pueden realizar mediante
punzonado cuando el agujero sea de un diámetro superior al espesor de la pieza,
que dicho espesor no sea superior a 15 mm y siempre que las piezas a unir no
estén sometidas a solicitaciones variables en el tiempo o cíclicas, que puedan
originar fenómenos de fatiga en la unión.
El diámetro estándar de los agujeros será igual al del vástago
del tornillo más:
- 1 mm para tornillos de 12 y 14 mm de diámetro;
- 1 ó 2 mm para tornillos de 16 a 24 mm;
- 2 ó 3 mm para tornillos de 27 mm o mayores.
Los agujeros de los tornillos de 12 y 14 mm también podrán tener
una holgura de 2 mm siempre y cuando la resistencia del grupo de tornillos a
aplastamiento sea inferior a la de cortante.
En uniones atornilladas resistentes por rozamiento pueden
emplearse agujeros a sobremedida o agujeros rasgados, cortos o largos, para
facilitar el montaje de las piezas.
Para agujeros a sobremedida, el diámetro del taladro será igual
al del vástago de los tornillos más:
- 3 mm para tornillos de 12 mm;
- 4 mm para tornillos de 14 a 22 mm;
- 6 mm para tornillos de 24 mm;
- 8 mm para tornillos de 27 mm o mayores.
Cuando se quiera permitir el movimiento relativo entre las
piezas a unir, se suele emplear agujeros rasgados. La anchura de los agujeros
rasgados cortos o largos en dirección normal al esfuerzo será igual al diámetro
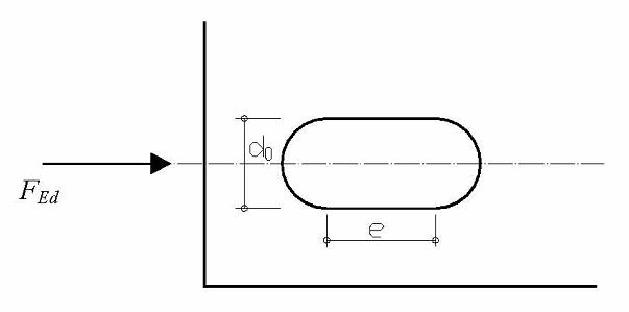
de los agujeros estándar correspondientes. En la dirección del esfuerzo, la
distancia e mostrada en la figura siguiente, para agujeros rasgados cortos será
igual a:
(d + 4) mm para tornillos de 12 ó 14 mm,
(d + 6) mm para tornillos de 16 a 22 mm,
(d + 8) mm para tornillos de 24 mm,
(d + 10) mm para tornillos de 27 mm y mayores.
Para agujeros rasgados largos será en todos los casos:
e=2,5*d mm, siendo d el diámetro del vástago del
tornillo correspondiente.
La distancia e1 desde el centro del agujero al
extremo frontal según la dirección de la transmisión de la carga será al menos
de 1,2*d0
e1 ≥ 1,2*d0
La distancia e2 del centro del agujero al
borde lateral medida normalmente a la dirección de la transmisión de la carga
será al menos de1,5*d0
e2 ≥ 1,5*d0
Si las piezas están expuestas a un ambiente agresivo u otras
influencias corrosivas, entonces las máximas distancias e1 y
e2 serán al menos: 40mm + 4*t (siendo t el
espesor más estrecho).
Para otros casos tomar e1 y
e2 ≤ 12*t ; 150mm
La distancia p1 entre centro de tornillos en
la dirección de la transmisión de la carga será al menos de
2,2*d0
p1 ≥ 2,2*d0
La separación p2 entre filas de tornillos,
medidos perpendicularmente a la dirección de la transmisión de la carga será al
menos de 3,0*d0
p2 ≥ 3,0*d0
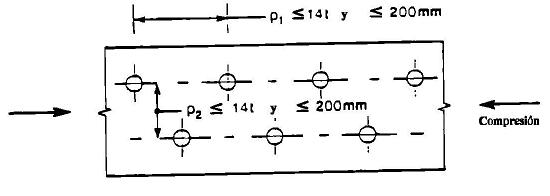
En el caso de elementos comprimidos, las separaciones
p1 y p2 no deberán superar al menor valor de
14*t ó 200 mm.
p1 ; p2 ≤ 14*t ó
200 mm
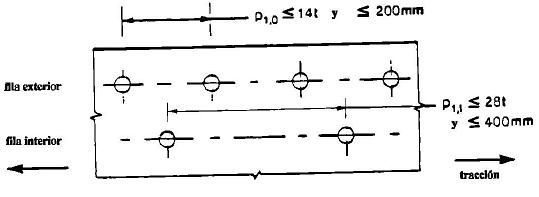
En el caso de elementos traccionados la separación
p1,i entre centros de tornillos en filas interiores puede ser
doble del valor dado para elementos comprimidos, siempre que la separación
p1,0 en la fila exterior en cada borde no supere el valor dado
para los elementos a compresión,
p1,i ≤ 28*t ó 400 mm, si se cumple
que p1,0 ≤ 14*t ó 200 mm
 +
+
Como norma general, en los montajes que se realicen los agujeros
para tornillos deben disponerse de forma que se dificulte la corrosión de las
piezas a unir y se permitan la colocación de los tornillos o bulones de una
manera fácil.
En la siguiente tabla y figuras que se exponen se establecen los
límites máximos y mínimos para las distancias entre agujeros y los bordes:
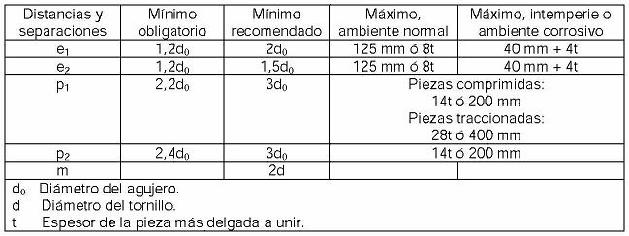
Fig.4 Disposiciones Constructivas
siendo,
e1: distancia desde el centro de un agujero a
un borde contiguo, medida en dirección del esfuerzo a transmitir;
e2: distancia desde el centro de un agujero a
un borde contiguo, medida en dirección perpendicular al esfuerzo a
transmitir;
p1: distancia entre centros de agujeros
contiguos, medida en dirección del esfuerzo a transmitir;
p2: distancia entre filas contiguas de
tornillos o roblones, medida en dirección perpendicular al esfuerzo a
transmitir;
m: distancia del eje del taladro a cualquier superficie
paralela a dicho eje.
En el caso de agujeros rasgados, las distancias
e1, e2, p1 y p2 se
medirán desde los centros de los semicírculos extremos.
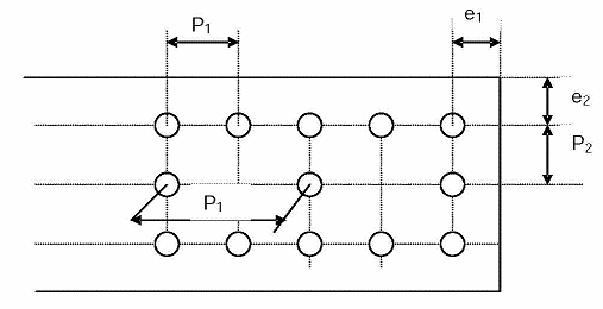
Fig.5 Distancias
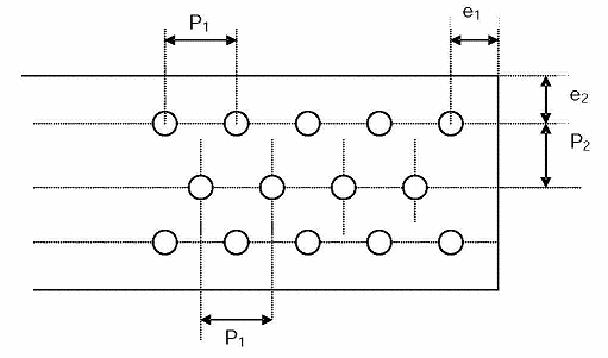
Fig.6 Agujeros al Tresbolillo
Para que los tornillos puedan apretarse sin dificultad, se
recomienda que la distancia m del eje del taladro a cualquier superficie
paralela a dicho eje no sea inferior a 2*d, siendo d el diámetro
del tornillo.
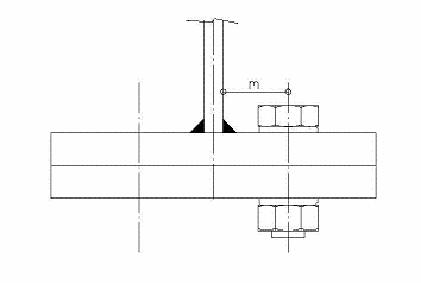
Fig.7 Distancia m
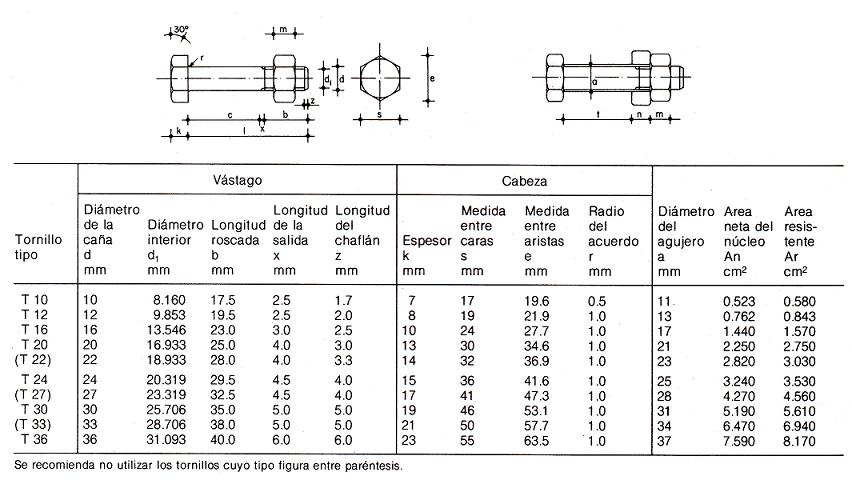
Se adjunta tabla con las características geométricas de los
tornillos ordinarios:
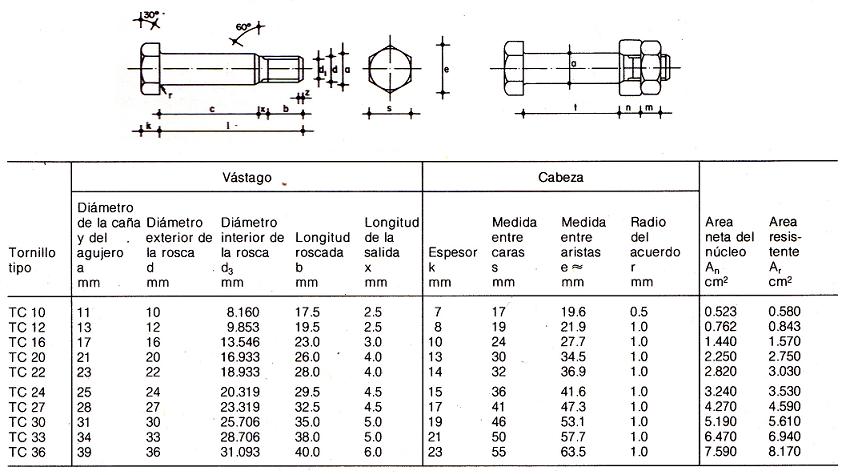
Se adjunta tabla con las características geométricas de los
tornillos calibrados:
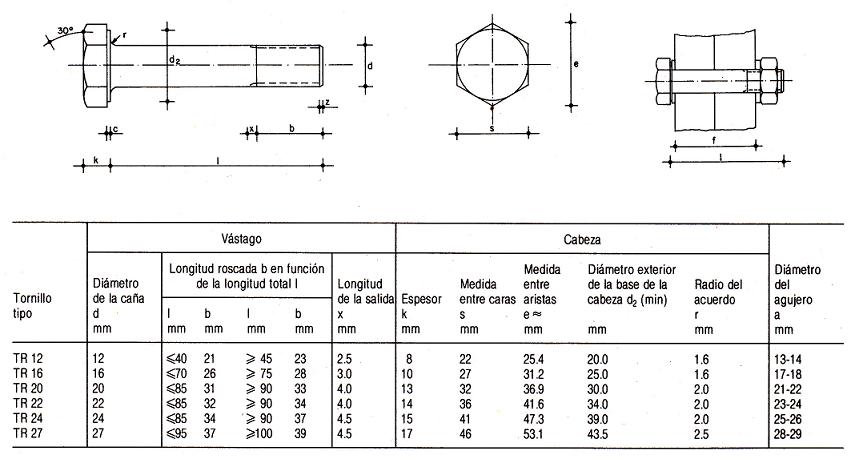
Se adjunta tabla con las características geométricas de los
tornillos de alta resistencia:
En función de la forma geométrica que presenta la rosca, se
pueden distinguir los siguientes tipos de roscas:
- agudas o de filetes triangular;
- trapezoidal;
- en diente de sierra;
- redondas;
- de filete cuadrado.
Las roscas del tipo agudas o triangulares quedan definidas por
el valor del diámetro exterior (d), del núcleo (d3) y
del de los flancos (d2), así como por el valor del ángulo de
los flancos de la rosca (alfa=60º, si se trata de la rosca triangular ISO) y por
último por la medida del paso (p)
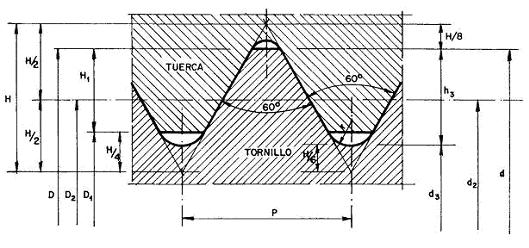
Fig.2 Rosca Triangular ISO
El paso de rosca es la distancia que existe entre dos crestas
consecutivas (p, en la figura anterior). Si el tornillo es de rosca
sencilla, por cada vuelta completa se corresponde con un avance del tornillo
igual al paso. Si es de rosca doble, el avance por cada vuelta será igual a dos
veces el paso.
Las roscas están normalizadas, existiendo dos tipos
fundamentales:
- la rosca Métrica ISO;
- la rosca Whitworth.
La diferencia entre ambos tipos de roscas son varias, como son:
- Para las roscas Métricas ISO, los ángulos de los las espiras
son de 60°, y los tornillos se redondea en el fondo de la rosca, mientras que
las puntas son planas como se aprecia en la figura anterior. Por el contrario,
para las roscas tipo Whitworth el ángulo de los flancos es de 55°, y tanto el
fondo como las puntas del fileteado en el tornillo van redondeados.
- Otra gran diferencia es que mientras en las roscas Métricas la
parte externa aplanada de los filetes está a una altura (o también llamada
profundidad del filete) h1=0,64595*p y el radio de giro de su
fondo redondeado vale r=0,1082*p, en las Whitworth tanto la punta
exterior como la parte interna son redondas, con altura o profundidad del filete
de valor h1=0,64033*p y radio de giro r=0,13733*p.
- En las roscas Métricas el paso se indica por el avance en
milímetros por cada vuelta, mientras en las Whitworth se da por número de hilos
por pulgada.
- Por último, las medidas nominales de la rosca, para el caso de
la rosca Métrica, se designa por el diámetro exterior de la rosca en mm. (si se
trata de Métrica fina se emplea en la designación, además del diámetro exterior
de la rosca, el valor del paso en mm.), mientras que para la rosca Whitworth, la
medida nominal de la rosca es el diámetro exterior en pulgadas.
Los tornillos ordinarios se designan por la sigla M,
aunque también pueden aparecer representados por la sigla T, seguidos por
el diámetro d de la caña, la longitud l del vástago, y por último
van seguidos de un número que especifica la calidad del acero.
Por ejemplo: Tornillo ordinario M 16x90-5.6 (significa
que se trata de un tornillo de 16 mm de diámetro de la caña, 90 mm de longitud
de vástago y fabricado en acero de calidad 5.6). También puede nombrarse de la
forma, T 16x90-5.6.
Los tornillos ordinarios tienen rosca triangular ISO de paso
grueso.

Fig.2 Rosca Triangular ISO
En los tornillos ordinarios el diámetro del agujero suele ser 1
mm más grande que el del vástago, aunque esta cifra es de referencia, por lo que
se remite al lector al apartado "4.2. Agujeros para tornillos" del presente
tutorial para obtener mayor información a este respecto.
Para el montaje de uniones con tornillos ordinarios se requiere
un menor ajuste entre el diámetro del tornillo y el del taladro (alrededor de 1
mm., como se ha dicho). Los tornillos ordinarios se suelen emplear para
transmitir esfuerzos por cortadura y de tracción principalmente, pero no para
momentos o pares de fuerzas, dado que la holgura existente ocasionaría que se
produjeran movimientos relativos entre las piezas.
Por otro lado, los tornillos calibrados se designan por la sigla
TC, aunque también pueden aparecer representados como en el caso anterior
por la sigla M (métrica), seguidos, al igual que los ordinarios por el
diámetro d de la caña, la longitud l del vástago, y por último,
seguidos de la numeración que especifica la calidad del acero empleado en la
fabricación del tornillo.
Los tornillos ordinarios y calibrados se diferencian básicamente
en sus características geométricas. Mientras que en los tornillos ordinarios el
diámetro del agujero es más o menos 1 mm más grande que el del vástago, en los
tornillos calibrados ambos diámetros están muy ajustados, por lo que se utilizan
con preferencia para la formación de nudos rígidos y en uniones de precisión,
que transmitan mayores esfuerzos sin que se produzcan desplazamientos relativos
entre las piezas.
Los tornillos de alta resistencia, o también llamados
pretensados, se designan por la sigla TR, o alternativamente también por
la sigla M (métrica), seguidos, al igual que los otros tipos de
tornillos, por el diámetro d de la caña y la longitud l del
vástago, seguidos del número que especifica la calidad del acero empleado en la
fabricación del tornillo. Ejemplo de designación de un tornillo pretensado o de
alta resistencia: M 20x55-10.9, o bien, TR 20x55-10.9.
Las uniones donde se han empleado tornillos pretensados trabajan
transmitiendo los esfuerzos por descompresión entre las superficies y por
rozamiento. Por tanto, en estas uniones implica la existencia de un estado de
compresión entre las superficies unidas, que junto al coeficiente de rozamiento
entre ellas, hace que se impida que exista cualquier desplazamiento relativo.
A continuación, en la siguiente tabla se exponen los
coeficientes de rozamiento obtenidos en función del tratamiento superficial que
tengan las chapas. En los dos primeros casos el chorreado o granallado implica
que debe obtenerse el grado Sa 21/2 según UNE-EN ISO 8504-1:
| Coeficientes de Rozamiento | ||
| Clase | µ | Tipo de Tratamiento |
| A | 0,50 | A1 - Chorreado o granallado sin picaduras de corrosión |
| 0,50 | A2 - Chorreado o granallado y metalizado por pulverización con aluminio | |
| 0,50 | A3 - Chorreado o granallado metalizados por pulverización a base de zinc, con ensayo de deslizamiento | |
| B | 0,40 | Chorreado o granallado con imprimación de pintura de silicato alcalino de zinc hasta un espesor de 80 µm |
| C | 0,30 | Limpieza por cepillado o flameo con eliminación de toda la cascarilla o herrumbre |
| D | 0,20 | Superficies no tratadas |
Las uniones ejecutadas con tornillos de alta resistencia,
TR, son uniones que resultan más rígidas, menos deformables y con mejor
comportamiento en estado límite de servicio, que las realizadas con tornillos
ordinarios o calibrados.
En estas uniones, al transmitirse los esfuerzos por rozamiento
entre las superficies, es muy importante aplicar el momento torsor o momento de
apriete adecuado para cada tornillo.
El par torsor de apriete aplicado a los tornillos induce en
éstos un esfuerzo de pretensado en la espiga del tornillo, que va a depender del
diámetro (d) y de un coeficiente (K). Este coeficiente K va
a tener en cuenta las características del rozamiento entre los componentes de la
parte que gira.
Para el caso que se empleen tuerca y tornillo ligeramente
engrasados, el par de apriete puede obtenerse aplicando la expresión
siguiente:
Mt=K*d*Fp,Cd
donde Fp,Cd es el esfuerzo axial de pretensado
en la espiga. Salvo indicación contraria que puedan marcar el Pliego de
Prescripciones Técnicas Particulares se considera que el esfuerzo de pretensado
que debe obtenerse de la espiga es el 70% de la resistencia a tracción del
tornillo (fub) multiplicada por el área resistente
(As), es decir, que el esfuerzo axial de pretensado viene dado
por la siguiente expresión:
Fp,Cd=0,7*fub*As,
que sustituyendo en la expresión primera, el momento de apriete
queda como:
Mt=K*d*0,7*fub*As
siendo, como ya se ha dicho:
K, coeficiente que depende de las condiciones de
suministro (K=0,18)
d, es el diámetro nominal del tornillo.
Aplicando la expresión anterior en un ejemplo, se podría
calcular el valor del momento de apriete aplicable a un tornillo TR12 de
clase 8.8. Sustituyendo valores se tiene que:
Mt= K*d*0,7*fub*As=
0,18*12*0,7*800*84,3= 101.969 Nmm
No hay comentarios:
Publicar un comentario